Hele Shaw Cell Experiment
Numerically simulate 2D Lennard-Jones Fluid using Fortran
Hele-Shaw Cell Experiment
1. Experiment Setup
- Glycerin and ink mixture placed between two acrylic plates, secured with four nails.
- Air injected into the plates, observing the Hele-shaw pattern.
- Four setups with different widths between the plates:
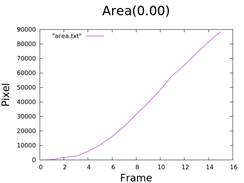
- No sticker: width of glycerin mixed ink
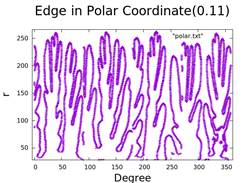
- Plastic sheet: 0.11cm
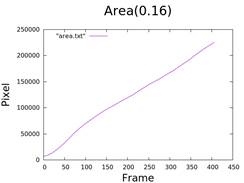
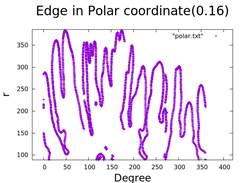
- One sticker: 0.16cm
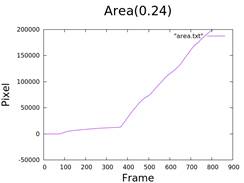
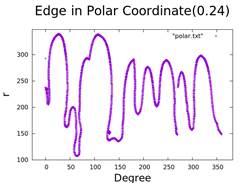
- Two stickers: 0.24cm
- Calculations include perimeter, area, length of fingers, number of fingers, and fractal dimensions.
2. Binary Every Frame and Reducing Noise
- Conversion of images to binary form (Figure 1 to Figure 2).
- Noise reduction using
Noise_Reduction.c&Circle_cut.c. - Edge extraction using
edge.c(Figure 3 to Figure 4). - Boundary determination and perimeter calculation.




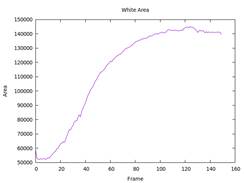
3. Calculate Area and Perimeter
- Using data from figures 3 and 4.
- Scripts used:
area.c&perimeter.c.
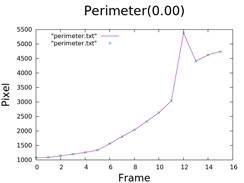
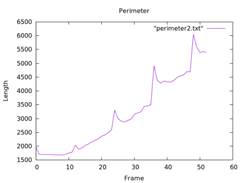
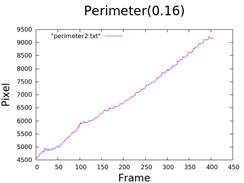
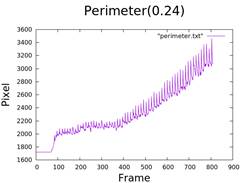
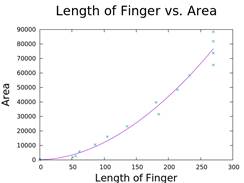
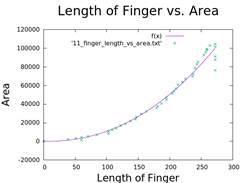
4. Calculate the Length of Fingers
- Technique involving minimizing a large circle until it touches the peripheral finger.
- Diagram of finger length over time.
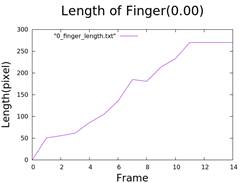
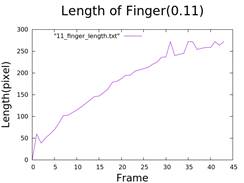
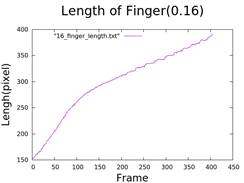
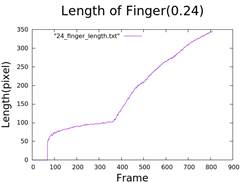
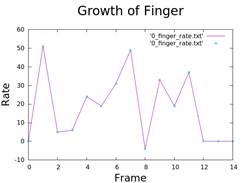
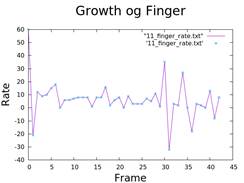
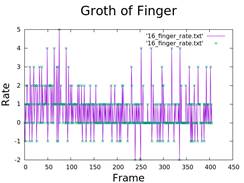
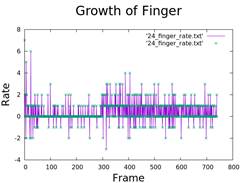
5. Calculate Injection Rate and Growth of Fingers
- Differentiation of area and radius over time.
- Analysis of viscosity and air injection rate.
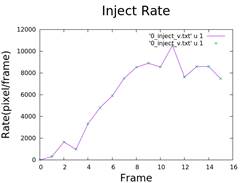
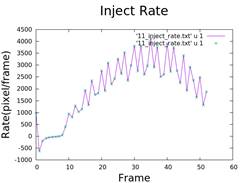
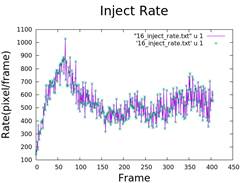
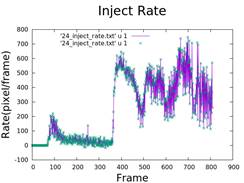
6. Fractal Dimension
- Scalar fractal analysis for dimension calculation.
- Method involves dividing the image into squares and counting those containing the pattern.
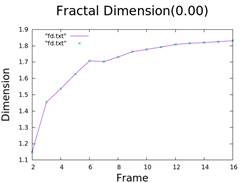
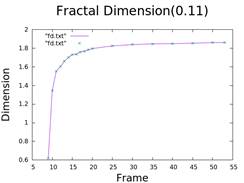
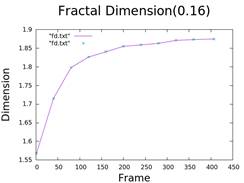
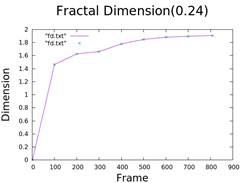
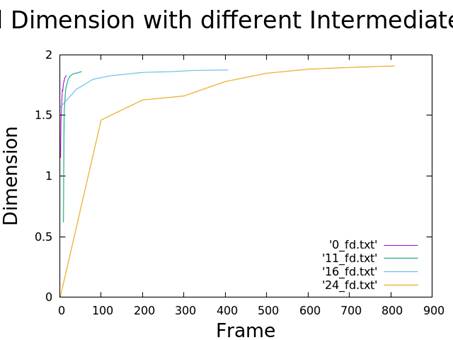
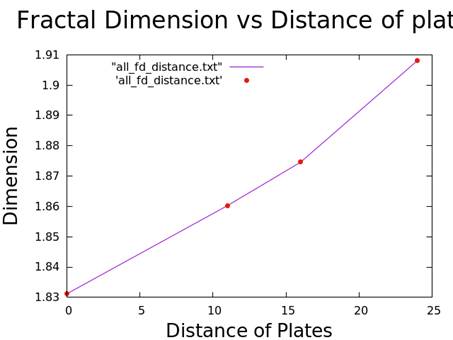
| Distance | Dimension |
|---|---|
| 0.0 | 1.8312 |
| 0.11 | 1.8603 |
| 0.16 | 1.8746 |
| 0.24 | 1.9081 |
7. Another Way to Calculate Fractal Dimension
- Assumption of Hele-Shaw pattern’s self-similarity.
- Radius and area used for dimensional analysis.
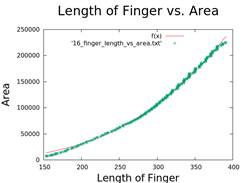
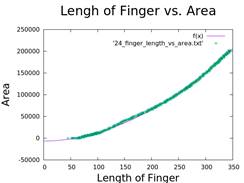
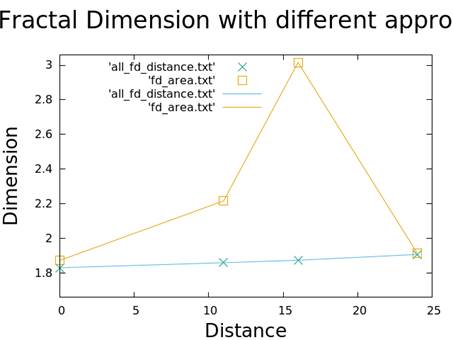
| Distance | Dimension(1) | Dimension(2) |
|---|---|---|
| 0.0 | 1.8312 | 1.87355 |
| 0.11 | 1.8603 | 2.21685 |
| 0.16 | 1.8746 | 3.01599 |
| 0.24 | 1.9081 | 1.91585 |
8. Hele-Shaw Cell in Polar Coordinate
- Analysis of injection rate and finger growth in polar coordinates.
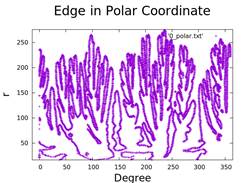




9. Number of Fingers and Difficulty
We try to use the result that we transform the experiment data to polar coordinate and calculate the number of finger with changing of time. Firstly, we try to find the slope where it is zero, but it didn’t get the accurate result from experiment. And then we try different method also want to calculate the number of fingers, but we didn’t success. The main reason is that the data are not continuous. So I think the next thing we need to do is use cubic spline method to make the data more smooth.
10. Additional Resources
- Video documentation and further analysis.